Question

The work of a student to solve a set of equations is shown:

Equation 1: m = 8 + 2n
Equation 2: 6m = 4 + 4n

Step 1:
−6(m) =  
−6(8 + 2n)
   [Equation 1 is multiplied by −6.]

6m =  
4 + 4n
   [Equation 2]

Step 2:
−6m =  
−48 − 12n
   [Equation 1 in Step 1 is simplified.]

6m =  
4 + 4n
   [Equation 2]

Step 3:
 −6m + 6m =  
−48 − 12n + 4n
   [Equations in Step 2 are added.]

Step 4:
0 =  
−48 − 8n


Step 5:
n =  
−6



In which step did the student first make an error?

Step 3
Step 5
Step 4
Step 2

Answer 1

Step 3

Explanation:

Answer 2

The answer is: "Step 3" .
_____________________________________________________
Note: "Step 3" incorrectly shows: "−6m + 6m = −48 − 12n + 4n " .
______________________________________________________
{Rather than the correct equation; which is:

" - 6m + 6m = - 48 – 12n + 4 + 4n " .}.
___________________________________________________
Note of interest:
___________________________________________________
Although not asked in the question/problem, let us continue with the correct equation; & to solve for" n ;


" - 6m + 6m = - 48 – 12n + (4 + 4n) ;

→ " 0 = - 48 – 12n + 4 + 4n " ;
__________________________
Combine the "like terms" on the "right hand side of the equation:
___________________________
-48 + 4 = -44 ;

- 12n + 4n = - 8n ;
__________________________

→ Rewrite the equation: " 0 = -8n – 44 " ;

↔ " - 8n – 44 = 0 " ;

Add "44" to each side of the equation;

→ -8n – 44 + 44 = 0 + 44 ;

to get:

→ -8n = 44 ;

Now, divide EACH SIDE of the equation by: "-8 " ;
to isolate "n" on one side of the equation; & to solve for "n" ;

→ -8n / 8 = 44 / 8 ;

→ n = 44/8 = (44 ÷ 4) / (8÷4) = 11/2 ;

n = "
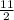`(11)/(2)`" ; or, write as: "5
`(1)/(2)`" ;

or, write as: " 5.5 " .
______________________________________________________