Question

Sec x -tan x sin x =1/secx

Help me prove it

Answer 1

L.H.S. =
`(1)/(cosx) -(sinx)/(cosx)sinx`

=
`(1)/(cosx) - (sin^2x)/(cosx)`

=
`(1-sin^x)/(cosx) = (cos^2x)/(cos x)`

= cos x = 1/secx

Answer 2

Explanation:

Hey there!

Given;

sec x - tan x . sin x = 1/(sec x).

~ Taking LHS.

= sec x - tan x . sin x

= 1/(cos x) - (sin x/cos x) . sin x { Using formula sec x = 1/cos x and tan x = (sin x/cos x)}

~ Multiply (sin x) and (sin x).

`= \frac{1 - { (\sin(x) )}^(2) }{ \cos(x) }`

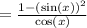
~ Use formula 1-sin²x= cos²x

`= \frac{ {cos}^(2) x}{ \cos(x) }`

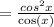
~ Cancel cos x.

= cos x

= 1/sec x { cos x = 1/sec x}

→ RHS proved.

Hope it helps.....