Answer:
The coordinates of the point R are (1,2).
Explanation:
Notice that we want to complete an internal division of the segment with endpoints
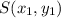 and
and
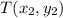 , in a given proportion m:n. This means, to find a point
, in a given proportion m:n. This means, to find a point
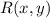 such that SR/RT = 1/2.
such that SR/RT = 1/2.
The formula to obtain the coordinates of the point
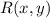 is:
is:
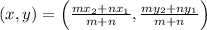 .
.
In our particular case
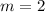 ,
,
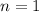 ,
,
 and
and
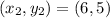 . Thus,
. Thus,
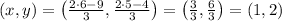 .
.