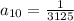Answer:
The nth term for the geometric sequence is given by:
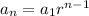 .......[1]
.......[1]
where,
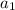 is the first term
is the first term
r is the common ratio of two consecutive terms
n is the number of terms.
Given the sequence:
625,125 25,...
This is a geometric sequence with first term(
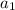 ) = 625
) = 625
and
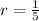
Since,
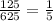 ,
,
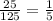 and so on...
and so on...
We have to find the 10th term of the given sequence
For n = 10
Substitute the given values in [1] we have;
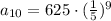
⇒
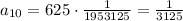
Therefore, the 10th term of the given sequence is,