Question

Please help quick

A rectangular garden has length twice as great as is width a second rectangular has the same length as the first garden and width that is 4 meters greater than width of the first garden the second garden has area of 120 square meters what is the length of the two gardens?

Answer 1

First garden information: let w = the width of the garden, then 2w = the length of the garden.

Second garden information:
(w + 4) = the width and 2w = the length; the area is equal to 120

Now taking the information of the second garden we can set up the following equation: 2w(w + 4) = 120 or the following quadratic 2w² + 8w - 120 = 0
Now solving this quadratic by factoring we see that the solutions are:
w = -10 and w = 6 ... of these two solutions only w = 6 makes sense.

With w = 6, the length of the two gardens would be 12

Answer 2

6 meters is the length of the two gardens

Explanation:

Bigger rectangle :

Width of the bigger rectangle = W

Length of the bigger rectangle : L = 2W

Smaller rectangle :

Width of the smaller rectangle : w = W+4

Length of the smaller rectangle :l = L = 2W

Area of the smaller rectangle, a =
`120 m^2`

`a=l* w`

`120 =(2W)* (W+4)`

`120 = 2w^2+8W`

`2W^2+8W-120=0`

`W^2+4W-60=0`

`W^2+10W-6W-60=0`

`W(W+10)-6(W+10)=0`

`(W+10)(W-6)=0`

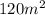
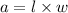
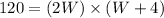
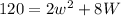
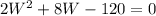
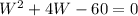
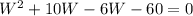
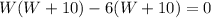
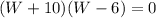
W = -10 (reject, negative)

W = 6

Length of the bigger rectangle : L = 2W = 2 × 6 m = 12 m

Length of the smaller rectangle : L = 2W = 2 × 6 m = 12 m

12 meters is the length of the two gardens