Question

S the system of equations is consistent, consistent and coincident, or inconsistent? y=−3x+1 2y=−6x+2 Select the correct answer from the drop-down menu.

consistent
consistent and coincident
inconsistent

Answer 1

We would know if a system is consistent, inconsistent, or coincident depending on the number of solutions it has. If it has only one solution, the system is said to be consistent. If it has none, the system is inconsistent; and if the system has an infinite number of solutions, it is said to be consistent and coincident.

Let's solve the system to know how many solutions it has.


`y=-3x+1`

`2y=-6x+2`

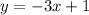
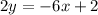
Notice that dividing the second equation by 2 would yield the exact same equation as 1. This would therefore allow us to conclude that AN INFINITE NUMBER of pairs of (x,y) coordinates would satisfy the system. Thus, the system is said to be consistent and coincident.

Answer 2

Ans: Consistent and Coincident

Step-by-step explanation:
First let me tell you the shortcut to know whether the system is consistent or inconsistent or coincident.

1) Consistent: If system of equations has at least one solution.
2) Inconsistent: If system of equations has no solutions.
3) Coincident: If one equation is multiple of the other.

Given Equations:
y=−3x+1 --- (A)
2y=−6x+2 --- (B)

As you can see equation (B) is same as equation (A):

`y = (-6x)/(2) + (2)/(2)`

=> y=−3x+1 (same as (A))

It means both the equations lie on top of one another in the graph. Therefore,
there are infinite solutions of the above system of equations.

Now apply the shortcut! As there are infinite solutions, it means the system is consistent.

Now let's see the coincident part.
Is one equation a multiple of second equation? YES! As,
equation-B = 2 * {equation-A)

Therefore, the system is coincident as well.

Hence the answer is: Consistent and Coincident

-i