Question

Suppose you invest $500 at an annual interest rate of 7.1% compounded continuously. How much will you have in the account after 4 years? Round the solution to the nearest dollar.

Answer 1

Answer: You will have $664.22 after 4 years of continuous interest.

To find the value of your investment using continuous interest, you have to use the equation: A = Pe^(rt)

Just plug in the values you know and evaluate:

A = 500e^(0.071x4)
A = $664.22 is the amount of your account after 4 years.

Answer 2

The amount in the account is $664.216

Explanation:

Given : Suppose you invest $500 at an annual interest rate of 7.1% compounded continuously.

To find : How much will you have in the account after 4 years?

Solution :

The formula of continuous compounding is

`A=Pe^(rt)`

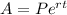
where,

A is the amount,

P is the Principal P= $500

r is the rate of interest = 7.1% = 0.071

t is the time period = 4 years

Substitute all the values in the formula,

`A=Pe^(rt)`

`A=(500)e^(0.071* 4)`

`A=(500)e^(0.284)`

`A=500* 1.328`

`A=664.216`

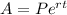
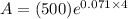
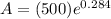
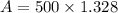
The amount in the account is $664.216

Round to nearest dollar = $664