Question

Complete the square to solve the equation below.check all that apply. x2 - 10x - 1 = 13

Answer 1

Complete square:
`(x-5)^2=39`

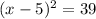
Solutions:
`x=5\pm√(39)`

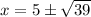
Explanation:

We have been given an equation
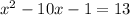`x^2-10x-1=13`. We are asked to complete the square.

First of all, we will add 1 to both sides of our given equation.

`x^2-10x-1+1=13+1`

`x^2-10x=14`

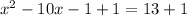
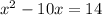
Now we will add
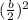`((b)/(2))^2` to both sides of our equation. We can see that the value of b is 10.

`((10)/(2))^2=5^2=25`

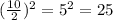
Upon adding 25 on both sides of our equation we will get,

`x^2-10x+25=14+25`

`x^2-10x+25=39`

`(x-5)^2=39`

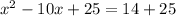
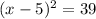
Taking square root of both sides we will get,

`(x-5)=√(39)`

`(x-5)=\pm√(39)`

`x-5=\pm√(39)`

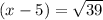
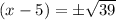
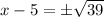
Adding 5 on both sides of our equation we will get.

`x-5+5=5\pm√(39)`

`x=5\pm√(39)`

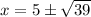
Therefore, solutions for our given equation are
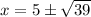`x=5\pm√(39)`.

Answer 2

x² -10x -1 = 13
x² -10x = 14
x² -10x +25 = 39 . . . . . add (10/2)² to complete the square
(x -5)² = 39
x -5 = ±√39
x = 5 ±√39