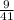Answer:
The value of trigonometric ratio
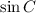 is
is
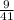
Explanation:
Given : Triangle ABC with right angle at B and BC = 80 and AC = 82
We have to find the value of trigonometric ratio
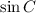
Consider the given triangle ABC,
We first draw the given right angled triangle ABC.
Also, given BC = 80 and AC = 82
We know, Trigonometric ratio sine gives relationship between perpendicular and hypotenuse.
That is
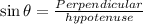
Here, For
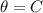
Perpendicular = AB and hypotenuse = AC
We first find AB
Using Pythagoras theorem,

H = 82, B = 80
Thus,
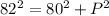
Simplify, we have,
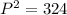
Thus, P = 18
Thus,

Thus, The value of trigonometric ratio
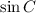 is
is