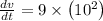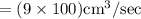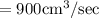Question

all edges of a cube are expanding at a rate of 3 centimeters per second. How fast is the volume changing when each edge is 10 centimeters?

Answer 1

Volume is changing by
`900 \mathrm{cm}^(3) / \mathrm{sec}`

Solution:

As per the problem, all edges of the cube are expanding at a rate of
`3 \mathrm{cm} / \mathrm{sec}`

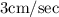
So,
`\left((d s)/(d t)\right)` =
`3 \mathrm{cm} / \mathrm{sec}`

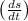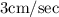
We also know that the volume
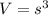`V=s^(3)`----- (i)

Differentiating the volume from equation (i) we get,

`(d v)/(d t)=3 s^(2) *\left((d s)/(d t)\right)`

`=\left(3 s^(2) * 3\right)`

`=9 s^(2)`

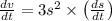
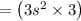
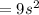
As given in the problem each edge = 10 cm.

Hence,
`(d v)/(d t)=9 *\left(10^(2)\right)`

`=(9 * 100) \mathrm{cm}^(3) / \mathrm{sec}`

`=900 \mathrm{cm}^(3) / \mathrm{sec}`