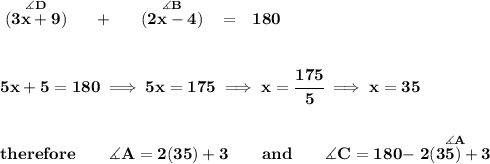Question

HEEELPPPPPP

Quadrilateral ABCD ​ is inscribed in this circle?

What is the measure of angle C?

Answer 1

not to bore you to death with the "inscribed quadrilateral conjecture", but you can do a quick search on google for it.

to make it short the conjecture says, that if the quadrilateral is inscribed in a circle, opposite angles are "supplementary angles", namely in this case ∡D + ∡B = 180°, and ∡A + ∡C = 180°.


`\bf \stackrel{\measuredangle D}{(3x+9)}~~~~+~~~~\stackrel{\measuredangle B}{(2x-4)}~~=~~180 \\\\\\ 5x+5=180\implies 5x=175\implies x=\cfrac{175}{5}\implies x=35 \\\\\\ therefore\qquad \measuredangle A=2(35)+3\qquad and\qquad \measuredangle C=180-\stackrel{\measuredangle A}{2(35)+3}`

Answer 2

the answer is 107

hope this helps