Question

Quadrilateral ABCD ​ is inscribed in this circle.

What is the measure of angle C?

Answer 1

B and D both sum to 180 (because their opposite arcs total 360, the whole circle), the rule is that "inscribed angles are 1/2 of their opposite arcs"

(3x+9) + (2x-4) = 180
5x + 5 = 180
5x +5 -5 = 180 -5
5x = 175
5x/5 = 175/5
x = 35
so now here's how we use the x,
angle A is opposite C, and their opposite arcs are touching and joining the circle, therefore
A + C = 180 [by the rule I explained before]
2x+3 + C = 180
2x+3 +C -C = 180 -C
2x+3 - 180 = 180-180 - C
2x-177 = -C
C = 177-2x = 177-2(35)
C = 177 - 70
C = 107°

Answer 2

Explanation:

We know that sum of the opposite angles of the quadrilateral inscribed in the circle is 180.

Thus, ∠B+∠D=180°

⇒
`3+9+2x-4=180`

⇒
`5x+5=180`

⇒
`5x=175`

⇒
`x=35`

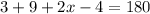
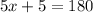
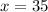
Now, substituting the value of x in ∠A, we have

∠A=
`2x+3=2(35)+3=73^(\circ)`

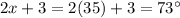
Again, sum of opposite angles of the quadrilateral inscribe in circle=180, thus

∠C+∠D=180°

⇒
`C+73=180`

⇒
`C=107^(\circ)`

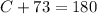
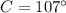
Therefore, the measure of ∠C is 107°.