Answer:
It does not have a solution.
Explanation:
To solve this you just need to arrange the equation into the general formula:
x^2-4x+5=0
So we just insert that into the general formula:
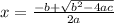
Now you just have to insert the values into this formula:
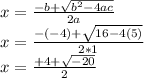
Since the square root is a negative number, you won´t be able to do that, so there is no solution for the equation.