Question

Malcolm and Robbie raced each other. The average of the maximum speed was 260 KM/hour. if doubled Malcolm’s maximum speed would be 80 KM/hour more than Robbys maximum speed. what were Malcolm’s and Robbie‘s maximum speed?

Answer 1

Maximum speed of Malcolm = 200 KM/hour

Maximum speed of Robby = 320 Km/hour

Explanation:

To solve this question we will form the equations as per statements given in the question.

Let the maximum speed of Malcolm is x KM/hour and Robbie's maximum speed be y KM/hour.

Now it given that average of maximum speeds of both is 260 KM/hour

So the equation will be
`(x+y)/(2)=260`

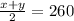
x + y = 260×2 = 520 ------(1)

It is given that if doubled Malcolm's maximum speed would be 80 KM/hour more than Robby's maximum speed.

2x = y + 80

2x - y = 80 --------(2)

Now we add equation 1 to equation 2

(x + y) + (2x - y) = 520 + 80

3x = 600

x = 200 KM/hour

Finally we put the value of x in equation 1

200 + y = 520

y = 520 - 200 = 320 KM/hour

Finally the answer is maximum speed of Malcolm is 200 KM/hour and maximum speed of Robby is 320 KM/hour

Answer 2

The correct answers are:

Malcolm's maximum speed is 200 km/hr and Robbie's is 320 km/hr.

Explanation:

Let R be Robbie's maximum speed and M be Malcolm's maximum speed. If Malcolm's speed is doubled (2M), it is 80 more than Robbie's (R+80); this gives us the equation
2M = R + 80.

We can isolate M by dividing both sides by 2:
2M/2 = R/2 + 80/2
M=R/2+40.

We know that their average is 260 km/hr. The average is found by adding the two maximum speeds together and dividing by 2:
(M+R)/2=260.

We will substitute our value for M from above:

`(((R)/(2)+40)+R)/(2)=260`

To solve this, we can multiply both sides by 2:

`(((R)/(2)+40)+R)/(2)* 2=260* 2 \\ \\(R)/(2)+40+R=520`

We can combine like terms, but to do that, we must write R as a fraction over 2. Since it is 1R, this is 2R/2:

`(R)/(2)+40+(2R)/(2)=520 \\ \\(3R)/(2)+40=520`

Subtract 40 from both sides:

`(3R)/(2)+40-40=520-40 \\ \\(3R)/(2)=480`

Now we will multiply both sides by 2:

`(3R)/(2)* 2=480* 2 \\ \\3R=960`

Divide both sides by 3:

`(3R)/(3)=(960)/(3) \\ \\R=320`

Plugging this into our first equation for M, we have:
M = R/2+40
M = 320/2+40
M = 160+40
M=200.