Question

A square has a diagonal with length 12.2. what is the area of the square to the nearest tenth?

Answer 1

Area of the square is 74.4 unit².

Explanation:

A square has a diagonal with length 12.2 units.

We have to find the area of the square.

Since all angles of a square are of 90° so by Pythagoras theorem

Side² + side² = Diagonal²

Let the length of the diagonal is d and length of sides be l.

l² + l² = d²

2l² = d²

`l^(2)=(d^(2) )/(2)=((12.2)^(2) )/(2)`

Since area of a square = side² = l²

Therefore area of square =
`(12.2^(2) )/(2)=(148.84)/(2)=74.42unit^(2)`

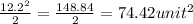
Area of the square is 74.4 unit².

Answer 2

The diagonal of a square is related to the length of the side of the square by

`d=\sqrt 2 L`
where d is the diagonal, and L the length of the side. We are told the diagonal of this square, d=12.2, so we can find the length of the side by rearranging the previous equation:

`L= (d)/( √(2) ) = (12.2)/( √(2) ) =8.6`

and now we can calculate the area of the square, which is given by the square of the length of the side:

`A=L^2=(8.6)^2=74.0`