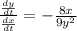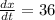Question

Assume x and y are both differentiable functions of t.

Answer 1

First Substitute x=-1 into the equation 4
`x^(2)` + 3
`y^(3)` = 28, and you get y=2.

Take the derivative of the equation 4
`x^(2)` + 3
`y^(3)` = 28, using implicit differentiation:

8x + 9
`y^(2)`
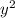
`(dy)/(dx)` = 0

Rearrange this in terms of
`(dy)/(dx)`:


`(dy)/(dx) = - (8x)/(9y^(2) )`

Keep in mind that
`(dy)/(dx)` is equal to
`( (dy)/(dt) )/( (dx)/(dt) )`

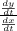
Substitute and you will get the following:


`( (dy)/(dt) )/( (dx)/(dt) ) = - (8x)/(9y^(2) )`

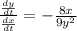
Put in the values for x, y, and
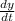
`(dy)/(dt)` and solve:


`( (dy)/(dt) )/( (dx)/(dt) ) = - (8x)/(9y^(2) )`


`(8)/( (dx)/(dt) ) = (8)/(36)`


`(dx)/(dt) = 36`