Question

What is the inverse of f if f (x) = ^3 sqrt x-7

Answer 1

Answer:
`f^(-1)(x)` =
`x^3+7`

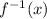Explanation:

Given f(x) =∛(x-7)

To find the inverse we have to make x as subject

Let f(x)= y

y=∛(x-7)

Taking cube both sides

y³=(∛(x-7))³

y³=x-7

Adding 7 both sides

y³+7=x-7+7

x=y³+7

Here we replace x with y and y with x

i.e. y=x³+7

Therefore
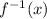`f^(-1)(x)`=
`x^3+7`

Answer 2

the inverse of the function given will be:
f(x)=(x-7)^(1/3)
to get the inverse we make x the subject
let f(x)=y=(x-7)^(1/3)
y=(x-7)^(1/3)
getting the cube of both sides we have:
y³=[(x-7)^(1/3)]³
y³=x-7
thus
x=y³+7
next we replace y by x and x with f^-1(x)
thus the inverse will be:
f^-1(x)=x³+7