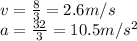Question

Circular Motion

The Trajectory of a mass point is a helix:
`r(t)=\left[\begin{array}{ccc}rcos(wt)\\rsin(wt)\\ht\end{array}\right]\\`
a) Compute the velocity v(t)=r(t) and the acceleration a(t).
b) What is the angel between the velocity and the acceleration?
c) If h=0, what is the radial acceleration and the velocity of the mass point at r=2m and 40rpm

No idea how to answer this question, I have never seen anything like it.
Any help would be awesome :)

Answer 1

Answer and step by step explanation:

First of all, I'm assuming you have had calculus, or this is going to be very awkward. Then, I'm replacing w with the Greek letter omega, it's a pet peeve of mine, sorry.

Shockingly, the derivative of a vector is computed by taking the derivative of each component (by linearity). If you've never heard the word derivative yet, you can think of the x and y components as two harmonic motions out of phase by 90°, and the z component as having constant speed h (harmonic motion is what you see when a mass moves along a circle with constant angular velocity and you look at it from the side).

At this point, let's use the derivative method for question a:

`v(t)=\dot{r}(t)=\left[\begin{array}{ccc}-\omega r\sin(\omega t)\\\omega r\ cos(\omega t)\\h\end{array}\right]; a(t)=\dot v(t)=\ddot{r}(t)=\left[\begin{array}{ccc}-\omega ^2r\cos(\omega t)\\-\omega ^2r\ sin(\omega t)\\0\end{array}\right]\\`

Point b requires computing angles, which screams dot product to me.

`\vec v(t) \cdot \vec a(t) =\left[\begin{array}{ccc}-\omega r\sin(\omega t)\\\omega r\ cos(\omega t)\\h\end{array}\right]\cdot \left[\begin{array}{ccc}-\omega ^2r\cos(\omega t)\\-\omega ^2r\ sin(\omega t)\\0\end{array}\right] = + \omega^3r^2 sin (\omega t) cos (\omega t) -\omega^3r^2 cos (\omega t) sin (\omega t) = 0 = ||\vec v|| ||\vec a|| cos \theta \implies cos\theta = 0 \implies \theta=\frac \pi2`

Now, the implied part is granted by the fact that we are assuming neither the velocity nor the acceleration are both zero, so the only option is for the cosine being zero, that makes the two vector orthogonal.

Finally, for point c, let's just take the moduli of both velocity and acceleration
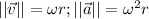`||\vec v|| = \omega r; ||\vec a||=\omega^2 r` and let's convert the angular velocity in civiliz... err, IS units:
`40 rpm = 40* (2\pi)/(60)rad/s = \frac 43 rad/s`

Let's replace and we get

`v=\frac83= 2.6 m/s\\a= \frac{32}3 = 10.5 m/s^2`