Question

A capacitor is formed from two concentric spherical conducting shells separated by vacuum. The inner sphere has radius 11.0 cm , and the outer sphere has radius 16.5 cm . A potential difference of 100 V is applied to the capacitor.

Part A
What is the energy density at r= 11.1 cm , just outside the inner sphere?
Part B
What is the energy density at r = 16.4 cm , just inside the outer sphere?
How can I solve this if I have no Q!

Answer 1

Part A)
First of all, let's convert the radii of the inner and the outer sphere:

`r_A = 11.0 cm = 0.110 m`

`r_B = 16.5 cm=0.165 m`
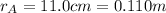
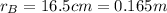
The capacitance of a spherical capacitor which consist of two shells with radius rA and rB is

`C=4 \pi \epsilon _0 (r_A r_B)/(r_B- r_A)=4\pi(8.85 \cdot 10^(-12)C^2m^(-2)N^(-1)) ((0.110m)(0.165m))/(0.165m-0.110m)=`

`=3.67\cdot 10^(-11)F`

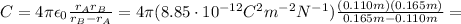
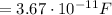
Then, from the usual relationship between capacitance and voltage, we can find the charge Q on each sphere of the capacitor:

`Q=CV=(3.67\cdot 10^(-11)F)(100 V)=3.67\cdot 10^(-9)C`

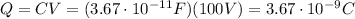
Now, we can find the electric field at any point r located between the two spheres, by using Gauss theorem:

`E\cdot (4 \pi r^2) = (Q)/(\epsilon _0)`
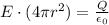
from which

`E(r) = (Q)/(4 \pi \epsilon_0 r^2)`
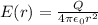
In part A of the problem, we want to find the electric field at r=11.1 cm=0.111 m. Substituting this number into the previous formula, we get

`E(0.111m)=2680 N/C`

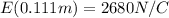
And so, the energy density at r=0.111 m is

`U= (1)/(2) \epsilon _0 E^2 = (1)/(2) (8.85\cdot 10^(-12)C^2m^(-2)N^(-1))(2680 N/C)^2=3.17 \cdot 10^(-5)J/m^3`

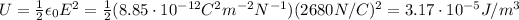
Part B) The solution of this part is the same as part A), since we already know the charge of the capacitor:
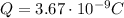
`Q=3.67 \cdot 10^(-9)C`. We just need to calculate the electric field E at a different value of r: r=16.4 cm=0.164 m, so

`E(0.164 m)= (Q)/(4 \pi \epsilon_0 r^2)=1228 N/C`

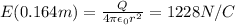
And therefore, the energy density at this distance from the center is

`U= (1)/(2)\epsilon_0 E^2 = (1)/(2) (8.85\cdot 10^(-12)C^2m^(-2)N^(-1))(1228 N/C)^2=6.68 \cdot 10^(-6)J/m^3`