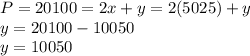Question

a farmer is fencing a rectangular area for his cattle and uses a straight portion of a river as one of the sides of the rectangle as Illustrated in the figure note that there is no fence along the river if the farmer has 20 100 feet of fence find the dimensions for the rectangular area that gives the maximum area for the cattle

Answer 1

If the width and the length of the rectangle are called x and y, the area is given by:

`A = xy`

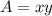
The perimeter of the rectangle is given by:

`P = 2x + y = 20100 feet`

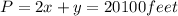
Combining both equations by eliminating the y variable:

`A = x(20100 - 2x) = 20100x - 2x^2`

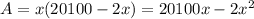
The maximum area can be found by taking the derivative with respect to x and setting it to zero.

`(dA)/(dx) = 20100 - 4x = 0`

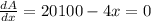
Solving for x:

`4x = 20100 \\ x = 5025`

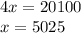
Solving for y:

`P = 20100 = 2x + y = 2(5025) + y \\ y = 20100 - 10050 \\ y = 10050`