Question

Find a model for simple harmonic motion if the position at t=0 is 5 centimeters, the amplitude is 5 centimeters, and the period is 4 seconds.

A) d=5cos(4t)
B) d=5sin(pi/2t)
C) d=4sin(5t)
D) d=5cos(pi/2t)

Answer 1

`\boxed{\boxed{D.\ d=5\cos \left((\pi)/(2)t\right)}}`

Explanation:

As at t=0 the amplitude is 5 cm, so the simple harmonic motion will be in cosine form. As in case of sine function, the value of function at x=0 is 0.

`\sin 0=0`

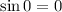
We know that, in the function

`y=a\cdot \cos b(x+c)+d`

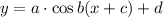
1. period is
   `(2\pi)/(b)`,
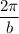2. horizontal shift or phase shift is c,
3. amplitude is a,
4. vertical shift is d.

As in this case the amplitude is given to be 5, hence
`a=5`

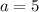
Also the period is given as 4, so

`\Rightarrow (2\pi)/(b)=4`

`\Rightarrow b=(2\pi)/(4)=(\pi)/(2)`

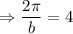
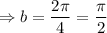
As nothing is given about the horizontal and vertical shift, so putting
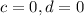`c=0,d=0`, the function becomes,

`y=5\cdot \cos (\pi)/(2)(x+0)+0`

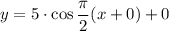
or
`y=5\cos \left((\pi)/(2)x\right)`

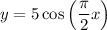
As in x axis time is taken as t and in y axis distance is taken as d, so the function becomes,

`d=5\cos \left((\pi)/(2)t\right)`