Answer: PQ = 18 unit.
Step-by-step explanation: Since, according to question,
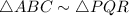 .
.
Therefore, by the property of similar triangles the ratio of corresponding sides must be equal.
Here, The right angle are at A in
 and at Q in
and at Q in
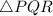 respectively.
respectively.
Moreover,
 is congruent to
is congruent to
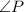 and
and
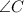 is congruent to
is congruent to
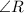 .
.
Therefore, AB, BC and AC are corresponding to sides PQ, QR and PR respectively.
Thus, we can write,
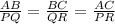
⇒
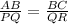
⇒
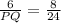 ( because, here, AB= 6, BC=8 and QR=24)⇒ PQ=18
( because, here, AB= 6, BC=8 and QR=24)⇒ PQ=18