Question

Cylinder A has radius r and height h as shown in the diagram. Cylinder B has radius 2r and height 2h. How many times greater is the surface area of Cylinder B than the surface area of Cylinder A?

Answer 1

Surface area of a cylinder: 2*pi*r^2+2*pi*r*h.
Surface area of Cylinder B: 2*pi*(2r)^2+2*pi*2r*2h
=8*pi*r^2+8*pi*r*h. Therefore Cylinder B is 4 times the surface area of cylender A

Answer 2

The surface area of cylinder B is four times of the surface area of cylinder A.

Explanation:

Since, the surface area of a cylinder is,

`A=2\pi R (R+H)`

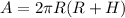
Where, R is the radius of the cylinder and H is the height of the cylinder,

For, cylinder A,

Radius = r,

Height = h,

Thus, the surface area of cylinder A,

`A_1=2\pi r(r+h)`

Similarly, For cylinder B,

Radius = 2r,

Height = 2h

`A_2=2\pi (2r)(2r+2h)=4[2\pi r(r+h)]`

`\implies A_2=4* A_1`

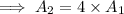
Hence, the surface area of cylinder B is four times of the surface area of cylinder A.