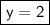Question

Which of the following ...

Answer 1

'parallel to the x-axis'. Parallel lines have the same slope. The x-axis is a horizontal line, and we know that horizontal lines have slopes of 0. Therefore this line must also have a slope of 0. We can plug this and the point into point-slope form to find the equation of the line.


`\sf y-y_1=m(x-x_1)`

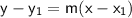
Where 'm' is the slope and (x1, y1) is a point on the line. Plug in what we know:


`\sf y-2=0(x-1)`

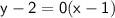
Distribute 0 in the parenthesis, we know that 0 times anything is 0, so the right side of our equation will be equal to 0:


`\sf y-2=0`

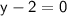
Add 2 to both sides:


`\boxed{\sf y=2}`