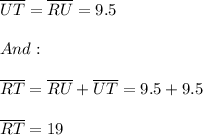Question

The diagonals of parallelogram QRST, TR and QS, intersect at point U. If RS = 10, ST = 12, and RU = 9.5, find the length of RT.

Answer 1

Two are the keys of this problem. First, a parallelogram is a quadrilateral (a polygon with four sides) where both pairs of opposite sides are parallel. Second, for every parallelogram its diagonals bisect each other, that is, each diagonal is divided into two equal parts. So, from the figure it is true that:

`\overline{RU}=\overline{UT} \\ \\ \overline{QU}=\overline{US}`

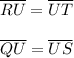
Since
`\overline{RU}=9.5`

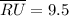
Then:

`\overline{UT}=\overline{RU}=9.5 \\ \\ And: \\ \\ \overline{RT}=\overline{RU}+\overline{UT}=9.5+9.5 \\ \\ \overline{RT}=19`