Question

The areas of two equilateral triangles are 27 yd2 and 75 yd2. Find the ratio of their perimeters.

Answer 1

If the areas of two equilateral triangles are 27 yd² and 75 yd², then the ratio of these areas is 27/75 = 9/25

If the ratios of the areas are 9:25, then their similarity ratio and the ratio of their perimeters is √9:√35 = 3:5.

3 : 5; 3 : 5 <==ANSWER

Answer 2

3:5

Explanation:

The areas of two equilateral triangles are 27 square yards and 75 square yards.

The area of an equilateral triangle with sides length 'a' is given by

`(\sqrt3)/(4)a^2`

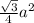
Therefore, we have

`((\sqrt3)/(4)a_1^2)/((\sqrt3)/(4)a_2^2)=(27)/(75)\\\\(a_1)/(a_2)=(3\sqrt3)/(5\sqrt3)`

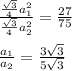
Now, multiply and divide both sides by 3

`(3a_1)/(3a_2)=(9\sqrt3)/(15\sqrt3)\\\\(P_1)/(P_2)=(9)/(15)\\\\(P_1)/(P_2)=(3)/(5)`

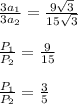
Hence, the ratio of perimeters of the given two equilateral triangles is 3:5