Answer:
The solutions are
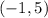 ,
,
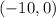 and
and
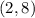
Explanation:
We have a system which is formed by the following equations :
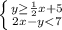
A solution to this system is a pair (x,y) that satisfies both equations.
In order to solve this exercise, we need to take each pair (x,y) and replace it in both equations. If the pair checks both equations therefore the pair (x,y) is a solution of the system.
The first pair is
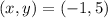
If we replace it in both equations :
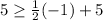 and also
and also

⇒
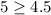
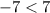
The pair (-1,5) satisfies both equations ⇒ It is a solution for the system.
The next pair is
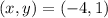
Replacing :
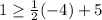
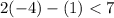
⇒

We find that it does not satisfy the first equation and therefore it can not be a possible solution to the system.
Now with
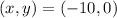
Replacing in the equations of the system :
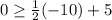
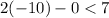 ⇒
⇒
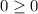
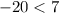
This pair satisfies both equations ⇒ The pair
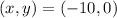 is a solution of the system.
is a solution of the system.
Now with
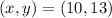
If we replace in the equations of the system :
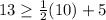
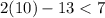 ⇒
⇒
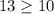
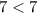
This pair satisfies the first equation but it does not satisfy the second one ⇒ It is not a solution of the system
The fifth pair is
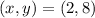
Using the equations of the system :
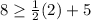 and
and

⇒
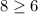
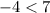
This pair verifies both equations ⇒ The pair
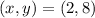 is a solution of the system.
is a solution of the system.
The final pair
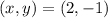
Replacing in the equations
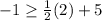
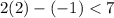
⇒
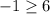 This inequality is wrong. Therefore the pair
This inequality is wrong. Therefore the pair
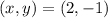 it is not a solution of the system.
it is not a solution of the system.
We conclude that the pairs
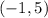 ,
,
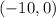 and
and
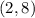 are solutions of the system above.
are solutions of the system above.