Question

Which of the following is a solution to 3tan^3x=tanx?

Answer 1

The given equation is:


`3 tan^(3)x=tanx \\ \\ 3 tan^(3)x-tanx=0 \\ \\ tanx(3 tan^(2)x-1)=0`

This means:

`tan(x)=0 \\ \\ x= tan^(-1)(0) \\ \\ x= \pi n`
where n is any integer.

&


`3 tan^(2)x-1=0 \\ \\ tan^(2)x = (1)/(3) \\ \\ tan(x) = +- \sqrt{ (1)/(3) } \\ \\ x= (5 \pi )/(6)+n \pi , ( \pi )/(6)+n \pi`

The values of x are the solutions to the given trigonometric equations.

Answer 2

Answer:
0, π, 2π, π/6, 5π/6, 7π/6 and 11π/6

Step-by-step explanation:
3 tan³x = tan x
3 tan³x - tan x = 0
tan x (3 tan²x - 1) = 0
either tan x = 0
This means that:
x = 0 , π or 2π ...........> I

or 3 tan²x - 1 = 0
This means that:
3 tan²x = 1
tan²x = 1/3
tan x = ±
`(1)/( √(3))`
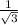at tan x =
`(1)/( √(3))`
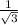
x = π/6 or 7π/6 ...................> II
at tan x = -
`(1)/( √(3))`
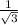
x = 5π/6 or 11π/6 ..............> III

From I, II and III, the solutions for x would be:
0, π, 2π, π/6, 5π/6, 7π/6 and 11π/6

Hope this helps :)