Question

(05.05)On a coordinate plane, the coordinates of vertices R and T for a polygon are R(−6, 2) and T(1, 2). What is the length of Side RT of the polygon?

Answer 1

Answer: The length of side RT is 7 units.

Step-by-step explanation: Given that the co-ordinates of vertices R and T for a polygon on a co-ordinates plane are R(−6, 2) and T(1, 2).

We are to find the length RT of the polygon.

We know that

the length of a line segment with endpoints P(a, b) and Q(c, d) is equal to the distance between the points P and Q.

By distance formula, the distance between P(a, b) and Q(c, d) is

`D=√((c-a)^2+(d-b)^2).`

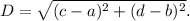
So, the distance between R(−6, 2) and T(1, 2) is given by

`RT=√((1+6)^2+(2-2)^2)=√(49+0)=7.`

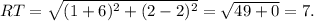
Thus, the length of side RT is 7 units.

Answer 2

The length of Side RT of the polygon is
`7\ units`

Explanation:

we know that

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

we have

`R(-6,2)\\T(1,2)`

substitute the values

`d=\sqrt{(2-2)^(2)+(1+6)^(2)}`

`d=\sqrt{(0)^(2)+(7)^(2)}`

`dRT=7\ units`