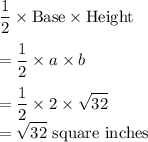Answer:
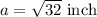
Rea of triangle =
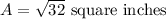
Explanation:
We are given the following information:
The lengths of the sides of a right angled triangle are a and b, and the hypotenuse is c.
b = 2 inch
c = 6 inch
We have to find the area of the triangle.
Since, the given triangle is a right angles triangle, it satisfies the Pythagoras theorem.
The Pythagoras statement states that:
- In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
Thus,

Area of triangle =