Answer:
Option (B) is correct.
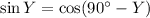
Explanation:
Given : A figure showing triangle XYZ with right angle at X and measurement of angles and sides are given.
We have to choose the correct option from the given options.
Consider the given options , we will check each one by one.
A)

We know, Cosine of an angle gives the relationship between base and hypotenuse.
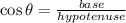
Thus, For
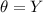 , we have base is z and hypotenuse = x
, we have base is z and hypotenuse = x
Thus,
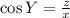
So, (A) is false.
B)
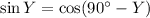
We know
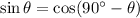
Thus,
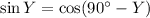 is true.
is true.
SO, (B) is correct.
C)
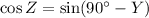
We know
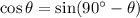
Thus,
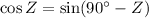
SO, (C) is not correct.
D)

Since,
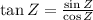
Thus,
 is incorrect.
is incorrect.
Thus, Option (B) is correct.