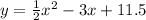Answer:
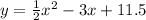
Explanation:
Vertex form of a quadratic equation;
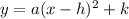
Vertex of the parabolas (h, k)
The vertex of the parabola is either the minimum or maximum of the parabola. The axis of symmetry goes through the x-coordinate of the vertex, hence h = -3. The minimum of the parabola is the y-coordinate of the vertex, so k= 7. Now substitute it into the formula;

Now substitute in the given point; ( -1, 9) and solve for a;
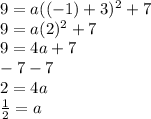
Hence the equation in vertex form is;

In standard form it is;