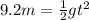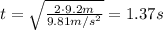The flowerpot is in free fall, so it moves by uniformly accelerated motion with acceleration equal to

. Its initial speed is zero, so we can write the law of motion for the pot as

where S(t) is the distance covered by the pot after a time t.
We want to find the time t at which the pot reaches ground, so the time t after which the pot has covered 9.2 m, therefore we should require S(t)=9.2 m and find t: