Answer:
The correct option is 1. The rate of change is 2%.
Step-by-step explanation:
The general growth function is
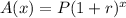 .... (1)
.... (1)
Where, P is initial value and r is rate of change.
The given exponential function for compounding interest is
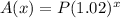
The given function can be written as
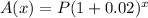 ..... (2)
..... (2)
From (1) and (2) we get
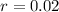
In % it can be written as
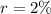
Therefore the correct option is 1. The rate of change is 2%.