Question

In the diagram AB, is divided into equal parts. The coordinates of point A are , and the coordinates of point I are .

Answer 1

We see that the relationship is linear. Let us calculate the slope of the curve. This is calculated by taking the slope relation for any 2 points. Here we pick F and D (x is the first coordinate):
λ=
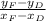
`(y_F-y_D)/(x_F-x_D)`=-2.25/1.75=9/7
We have that since this is a line, the vertical distance between F and D is the same as the vertical distance between any points that have a distance of 2 points. Hence the coordinates of point A can be calculated since it is moved by 1.75 left on the x-axis and 2.25 upwards in relation to D. Hence, A=(-8.75-1.75, -5.75+2.25)=(-10.50, 3.50). Every point going to the right is like adding (1.75/2, -2.25/2) to the coordinate of the point before it since the difference between two points is (1.75, -2.25). Hence, to get the coordinates of I, we take the immediate left of it, point H and we need to calculate: (-4.75+1.75/2, -9/25-2.25/2)=(-3.875, -10.375)

Answer 2

Ans:
Coordinates of Point A = (-10.0, -4.0)
Coordinates of Point I = (-3.875, -10.125)

Step-by-step explanation:

Analysis: WHEN MOVES UP, If we analyse the points H, F and G, we can see that the X value is decreased by 1.75 on every second point; whereas the Y value is increased by 1.75 on every second point.

Part-1: Coordinates of Point A
As the X value is decreased by 1.75 (WHEN MOVES UP) after every second point, therefore, the X coordinate of point A would be equals to the X coordinate of point D minus 1.75

=> X coordinate of Point A = -8.25 - 1.75 = -10.0

However, as the Y value is increased by 1.75 (WHEN MOVES UP) after every second point, therefore, the Y coordinate of point A would be equals to the Y coordinate of point D plus 1.75

=> Y coordinate of Point A = -5.75 + 1.75 = -4.0

Part-2: Coordinates of Point I
As the X value is decreased by 1.75 (WHEN MOVES UP) after every second point, therefore, the X coordinate of point I would be equals to the X coordinate of point H PLUS 1.75/2=0.875

=> X coordinate of Point I = -4.75 + 0.875 = -3.875

However, as the Y value is increased by 1.75 (WHEN MOVES UP) after every second point, therefore, the Y coordinate of point I would be equals to the Y coordinate of point H minus 0.875

=> Y coordinate of Point I = -9.25 - 0.875= -10.125