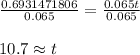It would take 10.7 years.
The formula for continuously compounded interest is:
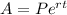
where P is the principal, r is the interest rate as a decimal number, and t is the number of years.
Using our information we have:
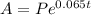
We want to know when it will double the principal; therefore we substitute 2P for A and solve for t:
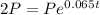
Divide both sides by P:
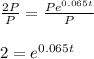
Take the natural log, ln, of each side to "undo" e:
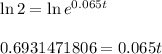
Divide both sides by 0.065: