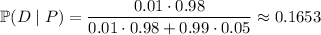1 Answer

Ask a Question

EthanB · Answer 1 · 2019-10-17T11:46:00+0000

Suppose

is the event that a given patient has the disease, and

is the event of a positive test result.

We're given that

$\mathbb P(D)=0.01$

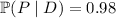
$\mathbb P(P\mid D)=0.98$

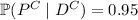
$\mathbb P(P^C\mid D^C)=0.95$

where
A^C

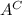
denotes the complement of an event

.

a. We want to find
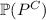
$\mathbb P(P^C)$ . By the law of total probability, we have

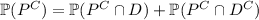
$\mathbb P(P^C)=\mathbb P(P^C\cap D)+\mathbb P(P^C\cap D^C)$

That is, in order for
P^C

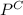
to occur, it must be the case that either

also occurs, or
D^C

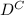
does. Then from the definition of conditional probability we expand this as

$\mathbb P(P^C)=\mathbb P(D)\mathbb P(P^C\mid D)+\mathbb P(D^C)\mathbb P(P^C\mid D^C)$

so we get

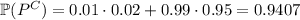
$\mathbb P(P^C)=0.01\cdot0.02+0.99\cdot0.95=0.9407$

b. We want to find
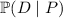
$\mathbb P(D\mid P)$ . Now, we can use Bayes' rule, but if you're like me and you find the formula a bit harder to remember, we can easily derive it.

By the definition of conditional probability,

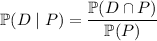
$\mathbb P(D\mid P)=(\mathbb P(D\cap P))/(\mathbb P(P))$

We have the probabilities of

/

occurring given that

/

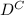
occurs, but not vice versa. However, we can expand the probability in the numerator to get a probability in terms of

being conditioned on

:

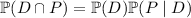
$\mathbb P(D\cap P)=\mathbb P(D)\mathbb P(P\mid D)$

Meanwhile, the law of total probability lets us rewrite the denominator as

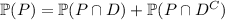
$\mathbb P(P)=\mathbb P(P\cap D)+\mathbb P(P\cap D^C)$

or in terms of conditional probabilities,

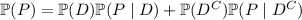
$\mathbb P(P)=\mathbb P(D)\mathbb P(P\mid D)+\mathbb P(D^C)\mathbb P(P\mid D^C)$

so that

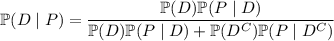
$\mathbb P(D\mid P)=(\mathbb P(D)\mathbb P(P\mid D))/(\mathbb P(D)\mathbb P(P\mid D)+\mathbb P(D^C)\mathbb P(P\mid D^C))$

which is exactly what Bayes' rule states. So we get

$\mathbb P(D\mid P)=(0.01\cdot0.98)/(0.01\cdot0.98+0.99\cdot0.05)\approx0.1653$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions