Question

The acid-dissociation constant for benzoic acid (c6h5cooh) is 6.3×10−5. calculate the equilibrium concentration of c6h5cooh in the solution if the initial concentration of c6h5cooh is 6.3×10−2 m .

Answer 1

`[C_6H_5COOH]_(eq)=0.06104M`

Step-by-step explanation:

Hello,

In this case, we properly write the undergoing dissociation reaction as follows:

`C_6H_5COOH<-->C_6H_5COO^-+H^+`

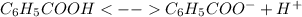
Know, by applying the law of mass action over this dissociation reaction, one obtains:

`Ka=([C_6H_5COO^-]_(eq)[H^+]_(eq))/([C_6H_5COOH]_(eq))`

Now, we have to notice that the equilibrium concentrations are given by the change
`x`, which alters the aforesaid equation in the following way, based on the ICE method:

`Ka=((x)(x))/((6.3x10^(-2)M-x))`

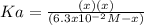
Now, solving for
`x`, we've got:

`Ka(6.3x10^(-2)M-x)=x^2\\6.3x10^(-5)(6.3x10^(-2)M-x)-x^2=0\\3.97x10^(-6)-6.3x10^(-5)x-x^2=0\\x_1=-0.0020M\\x_2=0.00196M`

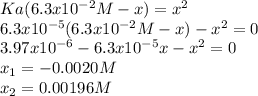
Finally, one computes the concentration of benzoic acid as;

`[C_6H_5COOH]_(eq)=0.0063M-0.00196M=0.06104M`

Best regards.

Answer 2

Answer is: the equilibrium concentration of benzoic acid is 0,06294 M.

Chemical reaction: C₆H₅COOH(aq) ⇄ H⁺(aq) + C₆H₅COO⁻(aq).
Ka(C₆H₅COOH) = 6,3·10⁻⁵.

c(C₆H₅COOH) = 6,3·10⁻² M.

[H⁺] = [C₆H₅COO⁻] = x; equilibrium concentration.
[C₆H₅COOH] = 0,063 M - x.
Ka = [H⁺] · [C₆H₅COO⁻] / [C₆H₅COOH].
0,000063 = x² / 0,063 M - x.
Solve quadratic equation: x = 0,00006 M.
[C₆H₅COOH] = 0,063 M - 0,00006 M.
[C₆H₅COOH] = 0,06294 M