Question

Which set of lengths cannot form a right triangle? a 20 mm, 48 mm, 52 mm b 10 mm, 24 mm, 26 mm c 11 mm, 24 mm, 26 mm d 5 mm, 12 mm, 13 mm?

Answer 1

Here some set of lengths given. We have to find which set of lengths can not form a right triangle.

To check whether it is a right triangle or not we will use Pythagoras theorem. If it holds true then the set will form a right triangle and if it is not true then it will not form a right triangle.

The Pythagoras theorem is
`c^2 = a^2+b^2`, where c = hypotenuse which is the largest length of the sides, a and b are other two sides.

The first set is, 20mm, 48mm, 52mm.

So here c = 52 as it is the largest side. We can take a and b any of the lengths 20 and 48. By substituting the values we will get,

`52^2 = 20^2 + 48^2`

`2704 = 400+2304`

`2704 = 2704`

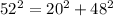
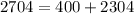
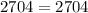
The Pythagoras theorem holds true here. So this set will form a right angled triangle.

The second set is, 10mm, 24mm, 26mm.

By substituting the values we will get,

`26^2 = 10^2 + 24^2`

`676 = 100+ 576`

`676 = 676`

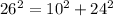
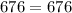
The Pythagoras theorem holds true here. So this set will form a right angled triangle.

The third set is, 11mm, 24mm, 26mm.

By substituting the values we will get,

`26^2 = 11^2+24^2`

`676 = 121 + 576`

`676 = 697`

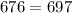
The Pythagoras theorem does not hold true here. So this set will not form a right angled triangle.

The fourth set is, 5mm, 12mm, 13mm.

By substituting the values we will get,

`13^2 = 5^2 + 12^2`

`169 = 25+144`

`169 = 169`

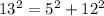
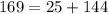
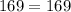
The Pythagoras theorem holds true here. So this set will form a right angled triangle.

We have got the required answer. Option C is correct here.

Answer 2

All of the sets of numbers have the ratio 5:12:13 except selection C, which cannot form a right triangle.