Question

If dy/dx=2xy^2 and y(-1)=2, find y(2)

Answer 1

This is a separable first order differential equation as an initial value problem.


`(dy)/(dx) =2xy^2`

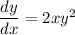
Divide both sides by y².


`(1)/(y^2)(dy)/(dx)=2x`

Multiply both sides by dx.


`(1)/(y^2) dy=2x * dx`

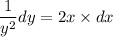
Integrate both sides.


`\int (1)/(y^2) dy= \int 2x * dx`


`- (1)/(y)=x^2+C`

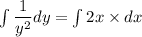
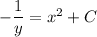
Multiply both sides by -1


`(1)/(y)=-x^2+C_1`
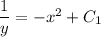
(where
`C_1=-C`)

Now, isolate y on one side of the equation.


`y=(1)/(-x^2+C_1)`

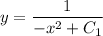
That's the general solution. Now, plug in the value x=-1 and y=2.


`2=(1)/(C_1-1)`


`C_1=3/2`

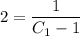
The final solution is the following:


`y=(1)/(-x^2+3/2)`

I hope this helps! If you need any clarifications, feel free to comment! :)