Question

The cannon on a battleship can fire a shell a maximum distance of 26.0 km.

(a) Calculate the initial velocity of the shell.

Answer 1

It is possible to demonstrate that the maximum distance occurs when the angle at which the projectile is fired is
`\theta = 45^(\circ)`.
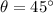
In fact, the laws of motions on both x- and y- directions are

`S_x(t)= v_0 cos \theta t`

`S_y(t)= v_0 \sin \theta t - (1)/(2) gt^2`
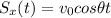
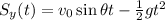
From the second equation, we get the time t at which the projectile hits the ground, by requiring
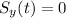
`S_y(t)=0`, and we get:

`t= (2 v_0 \sin \theta)/(g)`
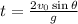
And inserting this value into Sx(t), we find

`S_x(t) = 2 (v_0^2)/(g) \sin \theta \cos \theta= (v_0^2)/(g) \sin (2\theta)`
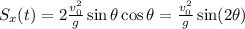
And this value is maximum when
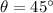
`\theta=45^(\circ)`, so this is the angle at which the projectile reaches its maximum distance.

So now we can take again the law of motion on the x-axis

`S_x(t)= (v_0^2)/(g) \sin (2\theta)`
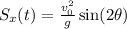
And by using
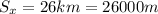
`S_x = 26 km=26000 m`, we find the value of the initial velocity v0:

`v_0 = \sqrt{ (S_x g)/(\sin (2\theta)) } = \sqrt{ ((26000m)(9.81m/s^2))/(\sin (2\cdot 45^(\circ))) } =505 m/s`