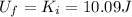We can use the law of conservation of energy to solve the problem.
The total mechanical energy of the system at any moment of the motion is:
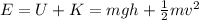
where U is the potential energy and K the kinetic energy.
At the beginning of the motion, the ball starts from the ground so its altitude is h=0 and therefore its potential energy U is zero. So, the mechanical energy is just kinetic energy:
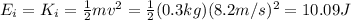
When the ball reaches the maximum altitude of its flight, it starts to go down again, so its speed at that moment is zero: v=0. So, its kinetic energy at the top is zero. So the total mechanical energy is just potential energy:

But the mechanical energy must be conserved, Ef=Ei, so we have
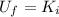
and so, the potential energy at the top of the flight is