Question

Triangle JKL has vertices J(2,4), K(3,1), and L(3,3). A translation maps the point J to J'(3,3).

What are the coordinates of K'?

Answer 1

To find the new coordinates of K, you compare the first and second x and y values for J.

The x value moved from 2 to 3 (over to the right 1), and the y value moved from 4 to 3(down 1 unit).

These same moves will happen with K.

So, 3 will move to 4 (x value) and 1 will move to 0 (y value).

The new coordinates for J are J(4, 0).

Answer 2

Answer: K'(4,0)

Explanation:

A translation is rigid transformation which moves the points of a figure about some distance in a certain direction on xy plane.

The translation rule for a figure moves r units to right and h units down is given by :-

`(x,y)\to(x+r,\ y-h)`

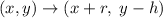
Given : Triangle JKL has vertices J(2,4), K(3,1), and L(3,3). A translation maps the point J to J'(3,3).

When we compare J(2,4) and J'(3,3), we can see that the J is moved 1 unit to the right (∵2+1=3) and 1 unit down (∵4-1=3) .

Translation rule for this translation:
`(x,y)\to(x+1,\ y-1)`

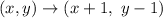
Then coordinates of K will be :

:
`K(3,1)\to K'(3+1,1-1)=K'(4,0)`

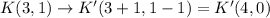
Hence, the coordinates of K' = K'(4,0)