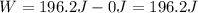Question

A 4 kg rock is dropped from 5 m. There is no friction. What kind of energy does is have before? What kind of energy does it have after? Was work done? Put the above into the law of conservation of energy.

Answer 1

1) The total mechanical energy of the rock is:

`E=U+K`
where U is the gravitational potential energy and K the kinetic energy.

Initially, the kinetic energy is zero (because the rock starts from rest, so its speed is zero), and the total mechanical energy of the rock is just gravitational potential energy. This is equal to

`E_i=U=mgh`
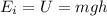
where
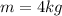
`m=4 kg` is the mass,
`g=9.81 m/s^2` is the gravitational acceleration and
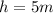
`h=5 m` is the height.
Putting the numbers in, we find the potential energy

`U=mgh=(4 kg)(9.81 m/s^2)(5 m)=196.2 J`

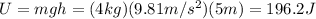
2) Just before hitting the ground, the potential energy U is zero (because now h=0), and all the potential energy of the rock converted into kinetic energy, which is equal to:

`E_f=K= (1)/(2)mv^2`
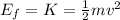
where v is the speed of the rock just before hitting the ground. Since the mechanical energy of the rock must be conserved, then the kinetic energy K before hitting the ground must be equal to the initial potential energy U of the rock:

`K=U=196.2 J`

3) For the work-energy theorem, the work W done by the gravitational force on the rock is equal to the variation of kinetic energy of the rock, which is:

`W=196.2 J-0 J=196.2 J`