Answer:- C is the right answer. The coordinates of the vertex = (h,k) = (6, −31).
Explanation:-
Given standard form :-
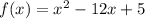
and its vertex form :-
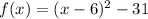 [which derived from the completing the square form.]
[which derived from the completing the square form.]
On comparing with the vertex form of equation in parabola =
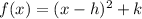
Then the coordinates of the vertex = (h,k) = (6, −31)
- A point (h,k) where a parabola intersects its axis of symmetry is called the vertex (h,k) of the parabola .