Question

This figure is made up of a quadrilateral and a semicircle.

What is the area of this figure?

Use 3.14 for pi. Round your final answer to the nearest tenth.


35.7 units²

51.4 units²

62.8 units²

82.8 units²

Answer 1

the answer is 35.7 units^2

Answer 2

Here the figure is made up of a quadrilateral and a semi circle.

ABCD is the quadrilateral here. We will find the sides of the quadrilateral by using the distance formula.

If (x₁, y₁) and (x₂, y₂) are two points given, then the distance between two points by using distance formula is,

`d =\sqrt({ x_(1)-x_(2))^2 +( y_(1) -y_(2) )^2}`

The co-ordinate of A is (-1,2) and co-ordinate of B is (-2,-1).

So the length of side AB =
`√((-1-(-2))^2+(2-(-1))^2)`

=
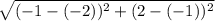
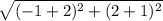`√((-1+2)^2+(2+1)^2)`(As negative times negative is positive)

=
`√((1)^2+(3)^2) =√(1+9) =√(10)`

The co-ordinate of C is (4,-3) and D is (5,0)

The length of side CD

=
`\sqrt(4-5)^2+(-3-0)^2}`

=
`√((-1)^2+(-3)^2)`

=
`√(1+9) =√(10)`

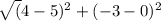
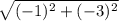
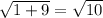
So the sides AB and CD are equal.

The length of side AD

=
`√((-1-5)^2+(2-0)^2)`

=
`√((-6)^2+(2)^2) =√(36+4) =√(40)`

The length of side BC

=
`√((-2-4)^2+(-1-(-3))^2)`

=
`√((-2-4)^2+(-1+3)^2)`

=
`√((-6)^2+(2)^2)=√(36+4) =√(40)`

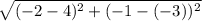
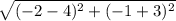
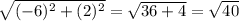
So the lengths of the sides AD and BC are equal.

So the quadrilateral is a rectangle whose length is
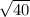`√(40)` and width is
`√(10)`.

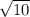Area of a rectangle = length × width

=
`(√(40)) (√(10))`

=
`√((40)(10))=√(400)`

=
`20 unit^2`

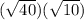
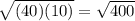
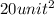
Now the diameter of the semicircle is the side AD =
`√(40)`

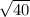
So, the radius of the semi-circle =
`(√(40))/(2)`

=
`(√((4)(10)))/(2)`

=
`((√(4))(√(10)))/(2)`

=
`(2√(10))/(2)` =
`√(10)`

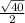
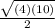
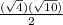
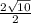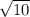
Area of semi-circle =
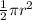`(1)/(2) \pi r^2`, where r is the radius.

=
`(1)/(2) \pi (√(10))^2`

=
`(1)/(2) \pi (10)`

=
`((\pi)(10))/(2)`

=
`(10\pi)/(2) = 5\pi` =
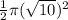
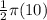
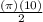
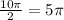`15.7 unit^2` ( Approximately taken to the nearest tenth)

Total area of the figure =
`(20+15.7) unit^2` =
`35.7 unit^2`

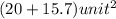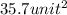
We have got the required answer.

Option a is correct here.