Question

What is the x intercept that is perpendicular to y=4/3x+1 and passes through (-4,9)

Answer 1

well, we know the line is perpendicular to that one above.... what is the slope of that one anyway? well, notice, the equation is already in slope-intercept form
`\bf y=\stackrel{slope}{\cfrac{4}{3}}x+1`.

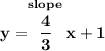
so, we're looking for the equation of a line perpendicular to that one, now, since that one has a slope of 4/3, a perpendicular line will have a negative reciprocal slope to that one,


`\bf \textit{perpendicular, negative-reciprocal slope for}\quad \cfrac{4}{3}\\\\ negative\implies -\cfrac{4}{ 3}\qquad reciprocal\implies - \cfrac{ 3}{4}`

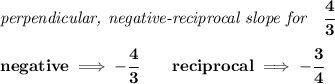
so, what is the equation of a line whose slope is -3/4 and runs through -4,9?


`\bf \begin{array}{ccccccccc} &&x_1&&y_1\\ &&(~ -4 &,& 9~) \end{array} \\\\\\ % slope = m slope = m\implies -\cfrac{3}{4} \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y- y_1= m(x- x_1)}\implies y-9=-\cfrac{3}{4}[x-(-4)] \\\\\\ y-9=-\cfrac{3}{4}(x+4)`

now, the x-intercept for any function is found by zeroing out the "y" and solving for "x", thus


`\bf y-9=-\cfrac{3}{4}(x+4)\implies 0-9=-\cfrac{3}{4}(x+4)\implies -9=-\cfrac{3x}{4}-3 \\\\\\ -6=-\cfrac{3x}{4}\implies -24=-3x\implies \cfrac{-24}{-3}=x\implies 8=x`

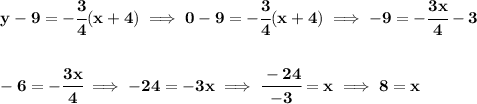
x = 8, y = 0 ( 8 , 0 )