Answer:
Hence, the minimum value of the function is 4.
Explanation:
We re given the function

Differentiating with respect to x, we get,

Equating f'(x) to 0, we have,
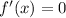
i.e.

i.e.

i.e.

Now, differentiating f'(x) with respect to x gives us,

Thus, the function f(x) have minimum at x= -5 and the minimum value is,
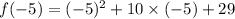
i.e.
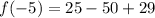
i.e.

i.e. f(-5) = 4
Hence, the minimum value of the function is 4.