Question

In a circle with a radius of 2.8 cm, an arc is intercepted by a central angle of π5 radians. What is the arc length?

Answer 1

Answer: The length of the arc is about 1.758 cm.

First, we need to determine the size of the angle. If we have pi/5 radians, we can convert that to 36 degrees, because pi radians is 180 degrees. Now, we know the measure of the arc is 36 degrees. 36 degrees out of 360 degrees is 10%.

Our arc is 10% of the circumference of the circle.

The circumference is 2(pi)r or 2(3.14)2.8 = 17.58 cm

Now, multiply 17.58 by 0.1 to get a total of 1.758 cm.

Answer 2

The correct answer is:

0.56π cm, or
1.7584 cm.

Step-by-step explanation:

The measure of an intercepted arc is the same as the measure of the central angle. The ratio of the arc to the entire circle is also the same as the ratio of the angle to the entire circle.

An entire circle is 2π radians. Our angle is π/5 radians. This gives us the ratio:

`((\pi)/(5))/(2\pi)=(\pi)/(5)* (1)/(2\pi)=(\pi * 1)/(5* 2\pi)=(\pi)/(10\pi)=(1)/(10)`

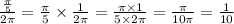
This means that the ratio of the arc to the entire circle is 1/10 also.

The circumference of a circle is given by the formula C=πd. We have the radius. The diameter is twice as long as the radius, so we multiply by 2:
2(2.8) = 5.6 cm.

This means the circumference is:
C = π(5.6) = 5.6π.

We want 1/10 of this:
1/10(5.6π) = 0.56π.

Using 3.14 for π, we have:
0.56(3.14) = 1.7584 cm.