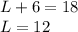Question

Gabriella is making monogrammed water bottles for a charity fundraiser. The first weekend, she sold 4 large water bottles and 3 small water bottles and raised $72. The second weekend, she sold 6 large water bottles and 2 small water bottles and raised $88.

How much did she charge for large water bottles?
How much did she charge for small water bottles?

What is the system of equations that models this situation?

Which of the following is a solution to the system: (a) $10 for large water bottles and $7 for small water bottles (b) $12 for large water bottles and $8 for small water bottles or (c) $9 for large water bottles and $9 for small water bottles?

Show your work.

Answer 1

Answer: B) A large bottle costs $12, and a small one costs $8.

Where L is how many large bottles have been sold, and is how many small bottles have been sold.

In order to find out how much money the large bottle and small bottles cost, we must solve the system of equations.

Step 1: Subtract 3S from both sides

`4L+3S=72\\4L=72-3S`

Step 2: Divide both sides by 44.

`4L=72-3S \\\\L=18-(3)/(4)S`

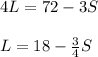
Step 3: Replace L for
`18-(3)/(4)S`

`6L+2S=88\\6(18-(3)/(4)S) +2S=88`

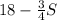
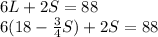
Step 4: Simplify

`6(18-(3)/(4)S)+2S=88\\108-4.5S+2S=88\\108-2.5S=88`

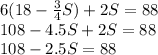
Step 5: Subtract 108 from both sides

`108-2.5S=88\\-2.5S=-20`

Step 6: Divide both sides by -2.5

`-2.5S=-20\\S=8`

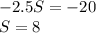
Step 7: Replace S for 8

`4L+3S=72\\4L+3(8)=72\\`

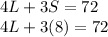
Step 8: Divide both sides by 4

`4L+24=72\\L+6=18`

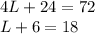
Step 9: Subtract 6 from both sides

`L+6=18\\L=12`